The Effect of Variable Microcurrents on EEG Spectrum and Pain Control
Heffernan, Michael. The Effect of Variable Microcurrents on EEG Spectrum and Pain Control. Canadian Journal of Clinical Medicine, 4(10):4-11, 1997. Download Article
50 subjects were evaluated in this 2 part double-blind study in which the researcher proposed a model of spectral smoothing using EEG (API Neurodata system) as a measure of regeneration and pain reduction. In phase 1, 2 minute spectral averages of root mean square EEG amplitude versus frequency were compared between 2 groups: a normal group of pain free persons (N=10), and an age (40 – 65 years old, mean of 60), sex matched group of pain patients with degenerative joint disease (N=10). The pain patients had at least 8 hours of pain per day for at least 2 years, and the pain-free subjects had no pain for 2 years. Pain-free subjects produced smooth declining spectral curves (mean deviation in RMS = 0.2, P>0.1), whereas the pain group showed many irregularities, and significant “unevenness” in EEG spectral arrays (mean deviation in RMS = 2.4, P>.01). On the basis of these findings and prior research the researcher proposed using spectral smoothness as a model to evaluate the effectiveness of differing microcurrent stimulators in safely treating pain patients.
In phase 2, 30 pain patients half males, half females, 30-65 years old, with at least 2 years of DJD of hip, shoulder, knee, or back, confirmed by X-ray, and unresponsive to medication, completed informed consent and were randomly assigned to 1 of 3 groups. Double blinding was achieved by placing the stimulators out of sight of both the investigator and subjects. They were each given a 5 minute test dose of stimulation from 3 differing stimulators, a 15 Hz, 500 Hz, and 15,000 Hz device (Liss Stimulator), a 0.5 Hz, random, biphasic device (Alpha-Stim), and a continuous 0.5 Hz device for control (BK Instruments). Using current limited, 500 µA stimulation bilaterally to the wrists, post stimulation spectral smoothing and pain control was found to be superior with the Alpha-Stim (deviation from normal FFT 3.1 pre to 0.4 post, P<.01). Although all 3 stimulators produced approximately a tenfold increase in RMS amplitude, the control 0.5 Hz device (deviation from normal FFT 2.7 pre to 2.6 post, P>0.1) and the Liss Stimulator (deviation from normal FFT 2.8 pre to 3.0 post, P>0.1) both produced considerable distortion from the EEG spectrum of normal, pain free subjects. Ordinal 5-point pain scales before and after stimulation showed that only the Alpha-Stim produced significant pain control with a five minute test dose 4.5 to 2.1, (P<.01), versus 4.3 to 4.5 (P>0.1) with the Liss Stimulator, and 4.6 to 4.8 (P>0.1) with the control device.
The researcher discusses these findings by proposing a theory of rapid pain control from regenerative restoration of normal cellular electrical fields. This theory of rapid pain reduction by electric field restoration is then contrasted with pain control by stress induction and increased production of endorphins. Finally the researcher discusses implications of using the spectral smoothing of both EEG and body fields as a model of reversing the negative, carcinogenic effects of externally applied extremely low frequency (ELF) when used therapeutically or delivered inadvertently from human electrical power usage. No side effects were reported.
NOT ALL WAVEFORMS ARE ALIKE!
The following charts are modified from Heffernan, 1997.
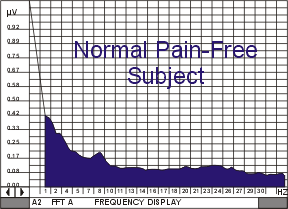 FIGURE 1: Two minute spectrum of EEG, frequency versus RMS amplitude, for a pain free normal subject. FIGURE 1: Two minute spectrum of EEG, frequency versus RMS amplitude, for a pain free normal subject. |
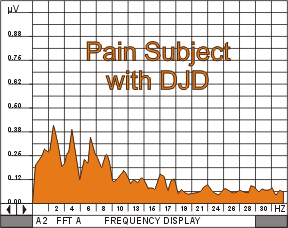 FIGURE 2: Two minute spectrum of EEG, frequency versus RMS amplitude, for a pain subject with DJD. FIGURE 2: Two minute spectrum of EEG, frequency versus RMS amplitude, for a pain subject with DJD. |
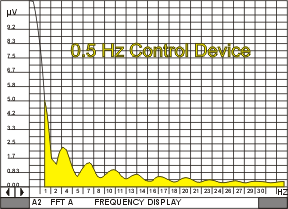 FIGURE 5: Two minute spectrum of EEG, frequency versus amplitude, of a subject while being treated with a 0.5 Hz, function FIGURE 5: Two minute spectrum of EEG, frequency versus amplitude, of a subject while being treated with a 0.5 Hz, functiongenerator. |
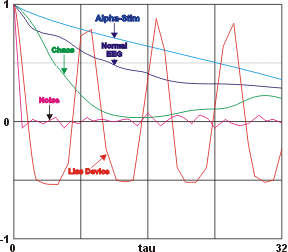 Correlation Function ExplanationThe correlation function is obtained by multiplying each X(t) by X(t-tau) and summing the result over all the data points. The sum is then plotted as a function of tau. This gives a measure of how dependent data points are on their neighbors. The value of tau at which the correlation function remains small is the correlation time. Correlation Function ExplanationThe correlation function is obtained by multiplying each X(t) by X(t-tau) and summing the result over all the data points. The sum is then plotted as a function of tau. This gives a measure of how dependent data points are on their neighbors. The value of tau at which the correlation function remains small is the correlation time. |
